find the subvector with max sum in a circular array

input: a circular array
output: a subvector of the array that has max sum

We can think that n elements are put on a circle and we want to find the subvector from the circle that has max sum.


Solution:
1. take any element as the leader and break the circle into one dimensional array a[1:n]. use the classical method to get the maxsum subvector
2. we did not consider the case that the maxsum subvector in the circle passes a[1]. in the next step we will figure out the maxsum subvector that passes a[1], suppose it is a[n - i:j].
3. claim: a[j+1:n-i-1] is the minsum subvector of a[1:n]. because sum of a[j+1:n-i-1] + sum of a[j+1:n-i-1] is fixed, one takes max means the other gets min.


Application:
find an index that the subvector starting from him always has sum greater than or equal to 0.


There are n gas stations posit... | CareerCup: "Bloomberg LP » Brain Teasers
DPS Prog on May 17, 2009 | Question #134799 (Report Dup) | Edit | History

There are n gas stations positioned along a circular road. Each has a limited supply of gas. You can only drive clockwise around the road. You start with zero gas. Knowing how much gas you need to get from each gas station to the next and how much gas you can get at each station, design an algorithm to find the gas station you need to start at to get all the way around the circle.
More Questions from this Interview
Filed Under: Bloomberg LP » Brain Teasers » Software Engineer / Developer


LOler on May 18, 2009 |Edit | Edit

O(n^2) time is easy. Start at each and just simulate it out.

O(n) time is possible, but I won''t spoil it for you.
Reply to Comment
CyberPhoenix on May 19, 2009 |Edit | Edit

Check Cormen for this, Its in exercise section of some chapters.....
Reply to Comment
Cookie on May 20, 2009 |Edit | Edit

Here is what Cormen has to say about the above problem but i quite well did not understand the solution..

The optimal strategy is the obvious greedy one. Starting will a full tank of gas,
Professor Midas should go to the farthest gas station he can get to within n miles
of Newark. Fill up there. Then go to the farthest gas station he can get to within n
miles of where he Þlled up, and Þll up there, and so on.
Looked at another way, at each gas station, Professor Midas should check whether
he can make it to the next gas station without stopping at this one. If he can, skip
this one. If he cannot, then Þll up. Professor Midas doesn’t need to know how
much gas he has or how far the next station is to implement this approach, since at
each Þllup, he can determine which is the next station at which he’ll need to stop.
This problem has optimal substructure. Suppose there are m possible gas stations.
Consider an optimal solution with s stations and whose Þrst stop is at the kth gas
station. Then the rest of the optimal solution must be an optimal solution to the
subproblem of the remaining m − k stations. Otherwise, if there were a better
solution to the subproblem, i.e., one with fewer than s −1 stops, we could use it to
come up with a solution with fewer than s stops for the full problem, contradicting
our supposition of optimality.
This problem also has the greedy-choice property. Suppose there are k gas stations
beyond the start that are within n miles of the start. The greedy solution chooses
the kth station as its Þrst stop. No station beyond the kth works as a Þrst stop,
since Professor Midas runs out of gas Þrst. If a solution chooses a station j < k as
its Þrst stop, then Professor Midas could choose the kth station instead, having at
least as much gas when he leaves the kth station as if he’d chosen the j th station.
Therefore, he would get at least as far without Þlling up again if he had chosen the
kth station.
If there are m gas stations on the map, Midas needs to inspect each one just once.
The running time is O(m).
Reply to Comment
Marian on May 26, 2009 |Edit | Edit

Cookie, no, that's not the problem. Therefore that's not the solution :))

I won't give the full solution how to do it in O(n), but I will provide all the hints.
The problem can be cast into a modified version of the very know problem: Maximum Consecutive Subsequence (of length 2*n-1). If during the search (in linear time for Maximum Consecutive Subsequence) you find a positive sum of length n, you found the solution to this problem.
Reply to Comment
karthikvaidy on June 12, 2009 |Edit | Edit

For each station, find (distance that can be traveled with gas available in that station - distance to next station). Create an array of these values and find the maximum positive consecutive substring. You have to start driving at the beginning of this substring.
PS: Remember that the stations are circularly arranged, so should the array. So it is possible for you to start on the 'last' station and still go around to all of them.
PPS: Another thing that can be done is to ensure that sum of all distances to be traveled is less than distance that can be traveled with available gas. Otherwise, it makes not difference where you start, you will get stranded.
Reply to Comment
Bajanfella on June 14, 2009 |Edit | Edit

Basically you have two arrays, gas_needed[n] and gas_at_station[n]. However, I would work with a third array which is the difference gas_needed - gas_at_station. Let's call this array gas_remaining[n](R[n])
Sum(Ri) where m is the nth consecutive station after i. i is the starting station if
i->m
the sum never goes negative.

O(m)
Reply to Comment
noname on July 10, 2009 |Edit | Edit

Bajanfella, Your algorithm is O(m^2) instead of O(m). Basically, you are just simulating with different starting points.
Reply to Comment
smartAss on July 17, 2009 |Edit | Edit

making use of a part of data str given by BajanFella, Lets take all the three arrays. Now in the arrya gas_remaining[] find the maximum subsequence which can be done in O(m), now starting at the first element of the subsequence solves the problem, thats it, we're done...
Reply to Comment
googler on August 13, 2009 |Edit | Edit

bejafella's answer is the correct one...and I must say this quite a popular interview question!
Reply to Comment
john on August 19, 2009 |Edit | Edit

yes, bejafella's got it
Reply to Comment
vipul k. on September 21, 2009 |Edit | Edit

if i have a car with 'zero' gas, how would i start the car in the first place???
Reply to Comment
S.M on October 01, 2009 |Edit | Edit

What if the gas tank is limited in capacity ?"

Fair division - Wikipedia, the free encyclopedia

Fair division - Wikipedia, the free encyclopedia

From Wikipedia, the free encyclopedia

Jump to: navigation, search

"Cake cutting" redirects here. For the wedding tradition, see Wedding reception#Wedding_cake.

Fair division, also known as the cake cutting problem, is the problem of dividing a resource in such a way that all recipients believe that they have received a fair amount. The problem is easier when recipients have different measures of value of the parts of the resource: in the "cake cutting" version, one recipient may like marzipan, another prefers cherries, and so on—then, and only then, the n recipients may get even more than what would be one n-th of the value of the "cake" for each of them. On the other hand, the presence of different measures opens a vast potential (a Pandora box) for many challenging questions and directions of further research.

There are a number of variants of the problem. The definition of 'fair' may simply mean that they get at least their fair proportion, or harder requirements like envy-freeness may also need to be satisfied. The theoretical algorithms mainly deal with goods that can be divided without losing value. The division of indivisible goods, as in for instance a divorce, is a major practical problem. Chore division is a variant where the goods are undesirable.

Fair division is often used to refer to just the simplest variant. That version is referred to here as proportional division or simple fair division.

Most of what is normally called a fair division is not considered so by the theory because of the use of arbitration. This kind of situation happens quite often with mathematical theories named after real life problems. The decisions in the Talmud on entitlement when an estate is bankrupt reflect some quite complex ideas about fairness,^[1] and most people would consider them fair. However they are the result of legal debates by rabbis rather than divisions according to the valuations of the claimants.

Berlin divided by the Potsdam Conference

Contents [hide] 1 Assumptions 2 Criteria for a fair division 3 Two players 4 Many players 5 Variants 6 History 7 In popular culture 8 See also 9 References 10 Further reading 11 External links

[edit] Assumptions

Fair division is a mathematical theory based on an idealization of a real life problem. The real life problem is the one of dividing goods or resources fairly between people, the 'players', who have an entitlement to them. The central tenet of fair division is that such a division should be performed by the players themselves, maybe using a mediator but certainly not an arbiter as only the players really know how they value the goods.

The theory of fair division provides explicit criteria for various different types of fairness. Its aim is to provide procedures (algorithms) to achieve a fair division, or prove their impossibility, and study the properties of such divisions both in theory and in real life.

The assumptions about the valuation of the goods or resources are:

• Each player has their own opinion of the value of each part of the goods or resources
• The value to a player of any allocation is the sum of his valuations of each part. Often just requiring the valuations be weakly additive is enough.
• In the basic theory the goods can be divided into parts with arbitrarily small value.

Indivisible parts make the theory much more complex. An example of this would be where a car and a motorcycle have to be shared. This is also an example of where the values may not add up nicely, as either can be used as transport. The use of money can make such problems much easier.

The criteria of a fair division are stated in terms of a players valuations, their level of entitlement, and the results of a fair division procedure. The valuations of the other players are not involved in the criteria. Differing entitlements can normally be represented by having a different number of proxy players for each player but sometimes the criteria specify something different.

In the real world of course people sometimes have a very accurate idea of how the other players value the goods and they may care very much about it. The case where they have complete knowledge of each others valuations can be modeled by game theory. Partial knowledge is very hard to model. A major part of the practical side of fair division is the devising and study of procedures that work well despite such partial knowledge or small mistakes.

A fair division procedure lists actions to be performed by the players in terms of the visible data and their valuations. A valid procedure is one that guarantees a fair division for every player who acts rationally according to their valuation. Where an action depends on a player's valuation the procedure is describing the strategy a rational player will follow. A player may act as if a piece had a different value but must be consistent. For instance if a procedure says the first player cuts the cake in two equal parts then the second player chooses a piece, then the first player cannot claim that the second player got more.

What the players do is:

• Agree on their criteria for a fair division
• Select a valid procedure and follow its rules

It is assumed the aim of each player is to maximize the minimum amount they might get, or in other words, to achieve the maximin.

Procedures can be divided into finite and continuous procedures. A finite procedure would for instance only involve one person at a time cutting or marking a cake. Continuous procedures involve things like one player moving a knife and the other saying stop. Another type of continuous procedure involves a person assigning a value to every part of the cake.

[edit] Criteria for a fair division

There are a number of widely used criteria for a fair division. Some of these conflict with each other but often they can be combined. The criterion are described here only for when each player is entitled to the same amount.

• A proportional or simple fair division guarantees each player gets his fair share. For instance if three people divide up a cake each gets at least a third by their own valuation.

• An envy-free division guarantees no-one will want somebody else's share more than their own.

• An exact division is one where every player thinks everyone received exactly their fair share, no more and no less.

• An efficient or Pareto optimal division ensures no other allocation would make someone better off without making someone else worse off. The term efficiency comes from the economics idea of the efficient market. A division where one player gets everything is optimal by this definition so on its own this does not guarantee even a fair share.

• An equitable division is one where the proportion of the cake a player receives by their own valuation is the same for every player. This is a difficult aim as players need not be truthful if asked their valuation.

[edit] Two players

For two people there is a simple solution which is commonly employed. This is the so-called divide and choose method. One person divides the resource into what they believe are equal halves, and the other person chooses the "half" they prefer. Thus, the person making the division has an incentive to divide as fairly as possible: for if they do not, they will likely receive an undesirable portion. This solution satisfies gives a proportional and envy-free division.

The article on divide and choose describes why the procedure is not equitable. More complex procedures like the Adjusted Winner procedure are designed to cope with indivisible goods and to be more equitable in a practical context.

Austin's moving-knife procedure^[2] gives an exact division for two players. The first player places two knives over the cake such that one knife is at the left side of the cake, and one is further right; half of the cake lies between the knives. He then moves the knives right, always ensuring there is half the cake – by his valuation – between the knives. If he reaches the right side of the cake, the leftmost knife must be where the rightmost knife started off. The second player stops the knives when he thinks there is half the cake between the knives. There will always be a point at which this happens, because of the intermediate value theorem.

The surplus procedure (SP) achieves a form of equitability called proportional equitability. This procedure is strategy proof and can be generalized to more than two people.^[3]

[edit] Many players

Fair division with three or more players is considerably more complex than the two player case.

Proportional division is the easiest and the article describes some procedures which can be applied with any number of players. Finding the minimum number of cuts needed is an interesting mathematical problem.

Envy-free division was first solved for the 3 player case in 1960 independently by John Selfridge of Northern Illinois University and John Horton Conway at Cambridge University. The best algorithm uses at most 5 cuts.

The first cake cutting procedure for 4 or more players that produced an envy-free division of cake for any number of persons was first published by Steven Brams and Alan Taylor in 1992.^[4] This number of cuts that might be required by this procedure is unbounded. A bounded moving knife procedure for 4 players was found in 1997.

There are no discrete algorithms for an exact division even for two players, a moving knife procedure is the best that can be done. There are no exact division algorithms for 3 or more players but there are 'near exact' algorithms which are also envy-free and can achieve any desired degree of accuracy.

A generalization of the surplus procedure called the equitable procedure (EP) achieves a form of equitability. Equitability and envy-freeness can be incompatible for 3 or more players.^[3]

[edit] Variants

Some cake-cutting procedures are discrete, whereby players make cuts with a knife (usually in a sequence of steps). Moving-knife procedures, on the other hand, allow continuous movement and can let players call "stop" at any point.

A variant of the fair division problem is chore division: this is the "dual" to the cake cutting problem in which an undesirable object is to be distributed amongst the players. The canonical example is a set of chores that the players between them must do. Note that "I cut, you choose" works for chore division.

Sperner's Lemma can be used to get as close an approximation as desired to an envy-free solutions for many players. The algorithm gives a fast and practical way of solving some fair division problems.^[5][6][7]

The division of property, as happens for example in divorce or inheritance, normally contains indivisible items which must be fairly distributed between players, possibly with cash adjustments (such pieces are referred to as atoms).

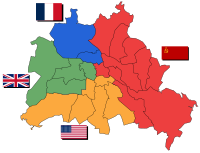
A common requirement for the division of land is that the pieces be connected, i.e. only whole pieces and not fragments are allowed. For example the division of Berlin after World War 2 resulted in four connected parts.

A consensus halving is where a number of people agree that a resource has been evenly split in two, this is described in exact division.

[edit] History

According to Sol Garfunkel, the cake cutting problem had been one of the most important open problems in 20th century mathematics,^[8] when the most important variant of the problem was finally solved together by Steven Brams and Alan Taylor in 1995.

Divide and choose has probably been used since prehistory. The related activities of bargaining and barter are also ancient. Negotiations involving more than two people are also quite common, the Potsdam Conference is a notable recent example.

The theory of fair division dates back only to the end of the second world war. It was devised by a group of Polish mathematicians, Hugo Steinhaus, Bronisław Knaster and Stefan Banach, who used to meet in the Scottish Café in Lvov (then in Poland). A proportional (fair division) division for any number of players called 'last-diminisher' was devised in 1944. This was attributed to Banach and Knaster by Steinhaus when he made the problem public for the first time at a meeting of the Econometric Society in Washington D.C. on 17 September 1947. At that meeting he also proposed the problem of finding the smallest number of cuts necessary for such divisions.

Envy-free division was first solved for the 3 player case in 1960 independently by John Selfridge of Northern Illinois University and John Horton Conway at Cambridge University, the algorithm was first published in the 'Mathematical Games' column by Martin Gardner in Scientific American.

Envy-free division for 4 or more players was a difficult open problem of the twentieth century. The first cake cutting procedure that produced an envy-free division of cake for any number of persons was first published by Steven Brams and Alan Taylor in 1992.

A major advance on equitable division was made in 2006 by Steven J. Brams, Michael A. Jones, and Christian Klamler.^[3]

[edit] In popular culture

In Numb3rs season 3 episode 'One Hour' Charlie talks about the cake-cutting problem as applied to the amount of money a kidnapper was demanding.

Hugo Steinhaus wrote about a number of variants of fair division in his book 'Mathematical Snapshots'. In his book he says a special 3 person version of fair division was devised by G. Krochmainy in Berdechów in 1944 and another by Mrs L Kott.^[9]

Martin Gardner and Ian Stewart have both published books with sections about the problem.^[10][11] Martin Gardner introduced the chore division form of the problem. Ian Stewart has popularized the fair division problem with his articles in Scientific American and New Scientist.

A Dinosaur comics strip is based on the cake-cutting problem.^[12]

[edit] See also

Adjusted Winner procedure Equity (economics) Game theory Justice (economics) Knapsack problem Nash bargaining game Sperner's lemma

Spite Steven Brams Topological combinatorics Tragedy of the anticommons Tragedy of the commons Weakly additive

[edit] References

1. ^ Game Theoretic Analysis of a bankruptcy Problem from the Talmud Robert J. Aumann and Michael Maschler. Journal of Economic Theory 36, 195-213 (1985)
2. ^ A.K. Austin. Sharing a Cake. Mathematical Gazette 66 1982
3. ^ ^{a b c} Brams, Steven J.; Michael A. Jones and Christian Klamler (December 2006). "Better Ways to Cut a Cake" (PDF). Notices of the American Mathematical Society 53 (11): pp.1314–1321. http://www.ams.org/notices/200611/fea-brams.pdf. Retrieved 2008-01-16.
4. ^ Steven J. Brams; Alan D. Taylor (January 1995). "An Envy-Free Cake Division Protocol". The American Mathematical Monthly (Mathematical Association of America) 102 (1): 9–18. doi:10.2307/2974850. http://www.jstor.org/pss/2974850. Retrieved 2008-11-15.
5. ^ Rental Harmony: Sperner's Lemma in Fair Division Francis Edward Su. Amer. Math. Monthly, 106(1999), 930-942. (based on work by Forest Simmons 1980)
6. ^ The Fair Division Calculator
7. ^ http://www.maa.org/mathland/mathtrek_3_13_00.html A Fair Deal for Housemates. Ivars Peterson's MathTrek. March 13, 2000
8. ^ Sol Garfunkel. More Equal than Others: Weighted Voting. For All Practical Purposes. COMAP. 1988
9. ^ Mathematical Snapshots. H.Steinhaus. 1950, 1969 ISBN 0-19-503267-5
10. ^ aha! Insight. Martin. Gardner, 1978. ISBN ISBN 978-0716710172
11. ^ How to cut a cake and other mathematical conundrums. Ian Stewart. 2006. ISBN 978-0199205905
12. ^ http://www.qwantz.com/archive/001345.html

[edit] Further reading

• Steven J. Brams and Alan D. Taylor (1996). Fair Division - From cake-cutting to dispute resolution Cambridge University Press. ISBN 0-521-55390-3
• Jack Robertson and William Webb (1998). Cake-Cutting Algorithms: Be Fair If You Can, AK Peters Ltd, . ISBN 1-56881-076-8.

[edit] External links

• Short essay about the cake-cutting problem by S. Abbas Raza of 3 Quarks Daily.
• Fair Division from the Discrete Mathematics Project at the University of Colorado at Boulder.
• The Fair Division Calculator (Java applet) at Harvey Mudd College
• Fair Division: Method of Lone Divider
• Fair Division: Method of Markers
• Fair Division: Method of Sealed Bids
• Vincent P. Crawford (1987). "fair division," The New Palgrave: A Dictionary of Economics, v. 2, pp. 274-75.
• Hal Varian (1987). "fairness," The New Palgrave: A Dictionary of Economics, v. 2, pp. 275-76.
• Bryan Skyrms (1996). The Evolution of the Social Contract Cambridge University Press. ISBN 9780521555838

海盗分金子 - 逻辑题

海盗分金子 - 逻辑题
数学的逻辑有时会导致看来十分怪异的结论。一般的规则是，如果逻辑推理没有漏洞， 那么结论就必定站得住脚，即使它与你的直觉矛盾。 1998年9月，加利福尼亚州帕洛阿 尔托的Stephen M. Omohundro寄给我一道难题，它恰好就属于这一类。这难题已经流传 了至少十年，但是Omohundro对它作了改动，使它的逻辑问题变得分外复杂了。

先来看看此难题原先的形状。10名海盗抢得了窖藏的 100块金子，并打算瓜分这些战利 品。这是一些讲民主的海盗（当然是他们自己特有的民主），他们的习惯是按下面的方式进行分配：最厉害的一名海盗提出分配方案，然后所有的海盗（包括提出方 案者本人）就此方案进行表决。如果50%或更多的海盗赞同此方案，此方案就获得通过并据此分配战利品。否则提出方案的海盗将被扔到海里，然后下提名最厉害 的海盗又重复上述过程。
所有的海盗都乐于看到他们的一位同伙被扔进海里，不过，如果让他们选择的话，他们还是宁可得一笔现金。他们当然也不愿意自 己被扔到海里。所有的海盗都是有理性的，而且知道其他的海盗也是有理性的。此外，没有两名海盗是同等厉害的——这些海盗按照完全由上到下的等级排好了座 次，并且每个人都清楚自己和其他所有人的等级。这些金块不能再分，也不允许几名海盗共有金块，因为任何海盗都不相信他的同伙会遵守关于共享金块的安排。这 是一伙每人都只为自己打算的海盗。
最凶的一名海盗应当提出什么样的分配方案才能使他获得最多的金子呢？

为方便起见，我们按照这些海盗 那优 程度来给他们编号。最怯懦的海盗为1号海盗，次怯懦的海盗为2号海盗，如此类推。这样最厉害的海盗就应当得到最大的编号，而方案的提出就将倒过来从上至下地进行。

分 析所有这类策略游戏的奥妙就在于应当从结尾出发倒推回去。游戏结束时，你容易知道何种决策有利而何种决策不利。确定了这一点后，你就可以把它用到倒数第 2次决策上，如此类推。如果从游戏的开头出发进行分析，那是走不了多远的。其原因在于，所有的战略决策都是要确定：“如果我这样做，那么下一个人会怎样 做？” 因此在你以下海盗所做的决定对你来说是重要的，而在你之前的海盗所做的决定并不重要，因为你反正对这些决定也无能为力了。

记住了 这一点，就可以知道我们的出发点应当是游戏进行到只剩两名海盗——即1号和2号——的时候。这时最厉害的海盗是2号，而他的最佳分配方案是一目了然 的：100块金子全归他一人所有，1号海盗什么也得不到。由于他自己肯定为这个方案投赞成票，这样就占了总数的50%，因此方案获得通过。现在加上3号海 盗。1号海盗知道，如果3号的方案被否决，那么最后将只剩2个海盗，而1号将肯定一无所获——此外，3号也明白1号了解这一形势。因此，只要3号的分配方 案，给1号一点甜头使他不至于空手而归，那么不论3号提出什么样的分配方案，1号都将投赞成票。因此3号需要分出尽可能少的一点金子来贿赂1号海盗，这样 就有了下面的分配方案： 3号海盗分得99块金子，2号海盗一无所获，1号海盗得1块金子。4号海盗的策略也差不多。他需要有50%的支持票，因此同3号一样也需再找一人做同党。 他可以给同党的最低贿赂是1块金子，而他可以用这块金子来收买2号海盗。因为如果4号被否决而3号得以通过，则2号将一文不名。因此，4号的分配方案应 是：99块金子归自己，3号一块也得不到，2号得1块金子，1号也是一块也得不到。5号海盗的策略稍有不同。他需要收买另两名海盗，因此至少得用2块金子 来贿赂，才能使自己的方案得到采纳。他的分配方案应该是：98块金子归自己，1块金子给3号，1块金子给1号?


这一分析过程可以照着上述思路继续进行下去。每个分配方案都是唯一确定的，它可以使提出该方案的海盗获得尽可能多的金子，同时又保证该方案肯定能通过。照这一模式进行下去，10号海盗提出的方案将是96块金子归他所有?

其他编号为偶数的海盗各得1 块金子，而编号为奇数的海盗则什么也得不到。
这就解决了10名海盗的分配难题。

Omohundro的贡献是他把这一问题扩大到有500名海盗的情形，即500名海盗瓜分100块金子。显然，类似的规律依然成立——至少是在一定范围内成立?
事实上，前面所述的规律直到第200号海盗都成立。 200号海盗的方案将是：
从1到199号的所有奇数号的海盗都将一无所获，而从2到198号的所有偶数号海盗将各得1块金子，剩下的1块金子归200号海盗自己所有。

乍 看起来，这一论证方法到200号之后将不再适用了，因为201号拿不出更多的金子来收买其他海盗。但是即使分不到金子，201号至少还希望自己不会被扔进 海里，因此他可以这样分配：给1到199号的所有奇数号海盗每人1块金子，自己一块也不要。202号海盗同样别无选择，只能一块金子都不要了——他必须把 这100块金子全部用来收买100名海盗，而且这100名海盗还必须是那些按照201号方案将一无所获的人。
由于这样的海盗有101名，因此 202号的方案将不再是唯一的——贿赂方案有101种。203号海盗必须获得102张赞成票，但他显然没有足够的金子去收买101名同伙。因此，无论提出 什么样的分配方案，他都注定会被扔到海里去喂鱼。不过，尽管203号命中注定死路一条，但并不是说他在游戏进程中不起任
何作用。相反，204号现 在知道，203号为了能保住性命，就必须避免由他自己来提出分配方案这么一种局面，所以无论204号海盗提出什么样的方案，203 号都一定会投赞成票。这样204号海盗总算 男拣到一条命：他可以得到他自己的1票、203号的1票、以及另外100名收买的海盗的赞成票，刚好达到保命所
需的50%。获得金子的海盗，必属于根据202号方案肯定将一无所获的那101名海盗之列。
205号海盗的命运又如何呢？他可没有这样走运了。他不能指望203号和204号支持他的方案，因为如果他们投票反对205号方案，就可以 以掷祸地看到205号被扔到海里去喂鱼，而他们自己的性命却仍然能够保全。这样，无论205号海盗提出什么方案都必死无疑。
206 号海盗也是如此——他肯定可以得到205号的支持，但这不足以救他一命。类似地，207号海盗需要104张赞成票——除了他收买的100张赞成票以及他自 己的1张赞成票之外，他还需3张赞成票才能免于一死。他可以获得205号和206号的支持，但还差一张票却是无论如何也弄不到了，因此207号海盗的命运 也是下海喂鱼。
208号又时来运转了。他需要104张赞成票，而205、206、207号都会支持他，加上他自己一票及收买的100票，他得以过 关保命。获得他贿赂的必属于那些根据204号方案肯定将一无所获的人（候选人包括2到200号中所有偶数号的海盗、以及201、203、204 号）。

现 在可以看出一条新的、此后将一直有效的规律：那些方案能过关的海盗（他们的分配方案全都是把金子用来收买100名同伙而自己一点都得不到）相隔的距离越来 越远，而在他们之间的海盗则无论提什么样的方案都会被扔进海里——因此为了保命，他们必会投票支持比他们厉害的海盗提出的任何分配方
案。得以避免葬身鱼腹的海盗包括201、202、204、208、216、232、264、328、456号，即其号码等于200加2的某一方幂的海盗。
现 在我们来看看哪些海盗是获得贿赂的幸运儿。分配贿赂的方法是不唯一的，其中一种方法是让201号海盗把贿赂分给1到199号的所有奇数编号的海盗，让 202号分给2到200号的所有偶数编号的海盗，然后是让204号贿赂奇数编号的海盗，208号贿赂偶数编号的海盗，如此类推，也就是轮流贿赂奇数编号和 偶
数编号的海盗。

结论是：当500名海盗运用最优策略来瓜分金子时，头44名海盗必死无疑，而456号海盗则给从1到199号中 所有奇数编号的海盗每人分1块金子，问题就解决了。由于这些海盗所实行的那种民主制度，他们的事情就搞成了最厉害的一批海盗多半都是下海喂鱼，不过有时他 们也会觉得自己很幸运——虽然分不到抢来的金子，但总可以免于一死。只有最怯懦的200名海盗有可能分得一份脏物，而他们之中又只有一半的人能真正得到一 块金子，的确是怯懦者继承财富。